Teoria dei numeri

L’oggetto di studio e i metodi usati determinano varie branche di questa disciplina. A Roma Tre ci occupiamo in particolare di Teoria Analitica dei Numeri, di Geometria Diofantea e di applicazioni alla Crittografia.
La Teoria Analitica dei Numeri usa principalmente metodi di analisi matematica per studiare varie proprietà (in particolare la distribuzione) di oggetti aritmetici come gli interi, i primi e le funzioni aritmetiche.
La Geometria Diofantea studia l’insieme delle soluzioni di un’equazione Diofantea, cercando di determinarne l’esistenza e, in caso affermativo, la cardinalità e la loro distribuzione. I metodi principali sono per lo più di natura geometrica, considerando le (eventuali) soluzioni come punti nelle varietà algebriche definite dalle equazioni stesse.
Molti protocolli e algoritmi in Crittografia sia classica che moderna si basano sulla Teoria dei Numeri.
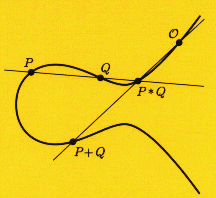
Il nostro gruppo di ricerca si interessa principalmente di crittografia post-quantum (cioè resistente agli attacchi del computer quantistico), in particolare di sistemi crittografici basati sulle isogenie tra curve ellittiche, una classe di curve algebriche molto importanti in Geometria Diofantea.

Dottorandi