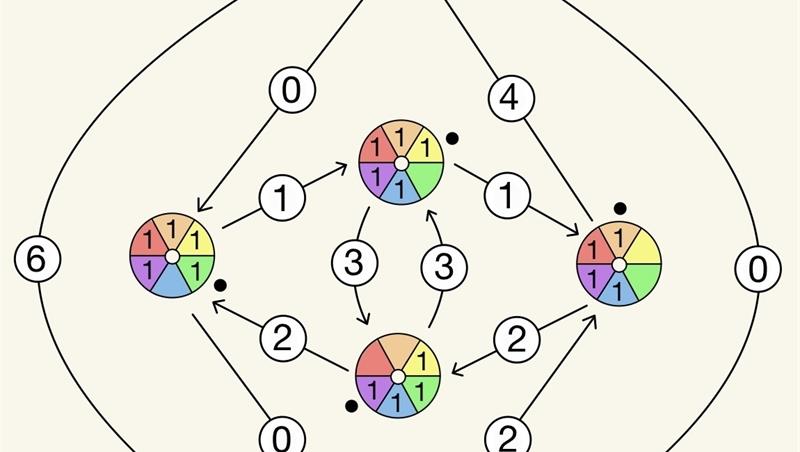
Abstract: Inspired by recent works exploring the interconnections between formal knot theory and quiver representation theory, we introduce new combinatorial objects generalizing the notion of a Kauffman state. A BMS state consists of a graph G embedded in an orientable surface, endowed with a nonnegative weight on the edges and a pair of integer-valued functions on the set of angles satisfying a balancing condition. Such an object is naturally associated with a representation of the Jacobian algebra of the medial quiver of G. After defining two symmetric notions of partial order for BMS states, we study the structure of the category in which these objects live, in connection with the lattices of subrepresentations arising from them. Furthermore, we address questions of decomposability. Finally, we discuss polynomial aspects and outline some open problems currently under investigation.
Il seminario è organizzato dai dottorandi di Matematica.
Link identifier #identifier__11560-1Sito web
This post is also available in:
Link identifier #identifier__49702-5 Eng
Eng